3. Das Stimmen der Orgel: Monochord und ZANGs Stimmpfeife
Das Stimmen von Musikinstrumenten ist, zu ZANGs Zeit ebenso wie heute, ein musiktheoretisches und ein praktisches Problem: Es gilt zu entscheiden, welche Stimmung (Temperatur) die richtige ist, und dann muss die ausgewählte Temperatur mit den verfügbaren technischen Mitteln auf das Instrument übertragen werden.
Die theoretische Frage entspringt dem Problem, dass man zwar für eine Tonart reine Intervalle stimmen kann, dass diese Stimmung aber für andere Tonarten nicht die richtigen Intervalle liefert und umso falscher klingt, je weiter die Tonart in der Quintenreihe entfernt ist. Die falschen Klänge werden traditionell „Wölfe“ genannt, und diese zu zähmen unternehmen die Musiktheoretiker des Barock große Anstrengungen. Für ZANG ist die Sache indes entschieden: Er referiert zwar die Namen FUX, MATTHESON, TELEMANN, KIRCHER, NEIDHARD, SPIESS, die in der Diskussion eine Rolle gespielt haben((zusammengefasst z.B. in SORGE 1748: „Gespräch zwischen einem Musico theoretico und einem Studioso musices von der Prätorianischen, Printzischen, Werckmeisterischen, Neidhardtischen und Silbermannischen Temperatur, Wie auch Von der neuen SYSTEMATE Herrn Capellmeister Telemanns, Zu Beförderung Reiner Harmonie entworffen von Georg Andreas Sorgen, Gräfl. Reuß-Plauischen Hof- und Stadt-Organisten zu Lobenstein, Wie auch der Societät der musikalischen Wissenschaften Mitglied. Lobenstein, im Verlag des Autoris“ (wer könnte der Versuchung widerstehen, diesen Titel ganz zu zitieren?); auch hier wird im Effekt die gleichschwebende Temperatur empfohlen, aber Für und Wider der verschiedenen Temperaturen wird abgewogen.)), aber er ist ein unbedingter Anhänger der gleichschwebenden Temperatur (üblicherweise mit dem Namen A. WERCKMEISTER verbunden), bei der das Pythagoräische Komma (der Unterschied zwischen 12 Quinten und 7 Oktaven, nämlich 531441/524288) auf die 12 Quinten aufgeteilt wird. Für noch verbliebene Anhänger mitteltöniger Stimmungen hat ZANG nur Spott übrig. Über den Verfasser eines 1792 erschienenen Orgelbuches, der die gleichschwebende Temperatur verwirft, heißt es in Kap. 1:
… so macht er, statt Rechnung, Zirkel und Maasstab, sein Gehör zum Oberrichter, und verweiset seine Wölfe, die er seinem Gehör nach, nicht verbannen kan, ins Dis, und vermuthlich mit ins Fis, Gis und H etc., wo sie ihre Zähne um so mehr bläcken, wenn ein geschickter Mann aus solchen Tönen spielt.((S. 2))
Mit den mathematischen Grundlagen und der Berechnung hält er sich nicht auf: die nötigen Zahlen entnimmt er den Veröffentlichungen von SORGE, von denen er die „Ausführliche Anweisung zur Razionalrechnung((Der volle Titel lautet: „Ausführliche und deutliche Anweisung zur Rational-Rechnung, und der damit verknüpfften Ausmessung und Abteilung des Monochords.“)) von Sorge, 8. Lobenstein, 1749“ ausdrücklich empfiehlt.
Das praktische Problem ist nun, die errechnete Stimmung auf die Orgel zu bringen. Davon der leichtere Teil ist die Einstimmung der ganzen übrigen Orgel von einer bereits temperiert gestimmten Oktave aus: Hier muss man nur reine Intervalle (Oktaven und Einklänge) stimmen, und da Schwebungen bei der Orgel gut hörbar sind, ist dieser Teil der Stimmarbeit zwar wegen der Menge der Pfeifen umfangreich, aber nicht schwierig. Der schwierige Teil ist die Temperierung der ersten, normalerweise der eingestrichenen Oktave. Es gibt, damals wie heute, zwei grundsätzliche Lösungen dafür:
a) Der Stimmer trainiert sein Gehör so gut, dass er temperierte Quinten hört und einstellen kann. Wenn man einmal einem Klavier- oder Orgelstimmer dabei zuhört, wie er die Temperierung im Quintenzirkel anlegt, bekommt man eine Vorstellung davon. Dies ist die Methode der Fachleute, und ZANG schildert sie im § 19 zum Abschluss der Orgelprobe.
… es ist, bey der razionalgleichen Temperatur, ein Komma Ditonikum in 12 gleiche Theile getheilt, wobey eine jede Quinte von den zwölfen, die innerhalb einer Octave liegen, um 1/12 eines Komma kleiner gemacht werden, daher die Quinten nicht ganz rein werden, sondern abwärts schweben müssen, dagegen werden die großen Terzen dadurch um so viel größer und höher schwebender [!], als jene abwärts schweben, wodurch man eine Temperatur erhält nach welcher man aus sämtlichen 24 Musiktönen, gleichlautend spielen kan. … 1.) Müßen alle C des zu probierenden Registers, ohne die geringste Schwebung zu hören, in den reinsten Octaven stehen. So dann
2.) Nimmt man das eingestrichne c‘ und seine Quinte g‘ eingestrichen, und hört, ob solche um 1/12 eines Komma, das ist ganz wenig abwärts schwebt? welches recht ist. …((S. 82))
Es geht weiter mit g‘-d“, d“-d‘, d‘-a‘, a‘-e“, e“-e‘ u.s.f. in temperierten Quinten und reinen Oktaven über h, fis, cis, gis, dis, b (erst hier die enharmonische Verwechslung!), f zurück zum c. Wenn man sehr gute Ohren oder Glück hat, kommt man beim f‘-c“ richtig heraus.
20.) Sollte diese letzte Quinte den andern nicht gleich seyn, und zu viel über oder unter sich schweben; so muß man nachsehen, wo gefehlet ist? und nachhelfen, bis diese letztere den vorigen Quinten gleich wird, das sich, bey einem guten Gehöre bald findet.((S. 84))
Man muss also bei dieser Methode ein gutes und trainiertes Gehör haben, dazu auch einige Geduld und Frustrationstoleranz, wenn man wieder „falsch herauskommt“.
b) Für Laien (zumindest) ist der zweite Weg erwägenswert, der zur Temperatur führt: Man verfertigt ein technisches Gerät (Instrument), das die errechneten Töne produziert, auf die man dann die Orgel (rein) einstimmen kann. Auf diesem Weg braucht man nicht ganz so gute Ohren, und deshalb wählen ihn ZANG und seitdem viele andere, wenn Laien stimmen sollen. Die modernste Version ist das elektronische Stimmgerät, bei dem die Frequenzen nach den Schwingungen eines Quartzes gesteuert werden. Zu ZANGs Zeiten ist Standard das Monochord, das seit alters in der Musiktheorie eine wichtige Rolle gespielt hatte.
Wie man ein Monochord herstellt und auf ihm die Marken für die richtige Einstellung des beweglichen Stegs auf die 12 Töne anbringt, wird in einem eigenen Kapitel (§ 21) dargestellt. ZANG folgt dem angegebenen Werk von SORGE. Mich hat ein wenig verwundert, dass das Monochord aus einem massiven Brett, also ohne Resonanzkasten hergestellt wird. Das verbessert zwar die Stabilität, aber der Klang wird recht leise. Als Ersatz sieht ZANG (wie SORGE) ein „Futteral“ vor, das bei Nichtgebrauch über das Monochord gestülpt wird, bei Bedarf aber darunter gestellt werden und so den Resonanzkasten ersetzen soll.((S. 103))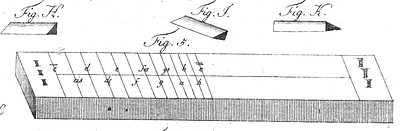
Das Monochord hat den Nachteil, dass sein Ton relativ schwach ist und schnell verklingt, so dass man langsame Schwebungen schwer oder nicht mehr hört. Schon vor ZANG wurden daher Stimmpfeifen((Im Orgelbaumuseum zu Ostheim v.d. Rhön wird so eine Stimmpfeife gezeigt. Im Unterschied zur von ZANG vorgeschlagenen ist sie von rundem Querschnitt und dazu bestimmt, in ein Register eingestellt zu werden.)) vorgeschlagen, nämlich gedackte Pfeifen, deren Tonhöhe durch Verschieben des Deckels in der Pfeife verändert werden kann; jedem Ton der chromatischen Leiter entspricht dann eine bestimmte Position des Deckels. SORGE((A. SORGE 1758: Zuverlässige Anweisung, Claviere und Orgeln behörig zu temperieren und zu stimmen. Leipzig und Lobenstein. Den Hinweis verdanke ich dem Orgelbaumuseum Ostheim.)) sieht Stimmpfeifen für jedes einzelne Orgelwerk (wegen des verschiedenen Winddruckes) vor. Man hat sich das so vorzustellen, dass aus einem bestimmten Register des Orgelwerks zunächst 1 bestimmte Pfeife entnommen und durch die Stimmpfeife ersetzt wird. An dieser werden dann die temperierten Töne eingestellt und nach diesen die Oktave gestimmt, von der aus dann alle andern Pfeifen des Werks gestimmt werden. Die SORGEsche Stimmpfeife wird also in ein Orgelregister gestellt und bekommt Orgelwind. Ob ZANG dieses Buch SORGEs gekannt hat, ist ungewiss; er schreibt nichts davon. Die von ihm vorgeschlagene Stimmpfeife unterscheidet sich jedenfalls von der SORGEschen dadurch, dass sie „Nach der Invention des Herrn Voits“((S. 109; J. M. VOIT, ZANGs Gewährsmann für den Orgelbau, s.o.)) eine eigene Windversorgung hat, einen der Figur nach ansehnlichen Doppelbalg, der dafür sorgt, dass die Pfeife eine ausreichende Zeit lang klingt. Der Apparat ist andererseits klein genug, um ihn zum Stimmen mit in das Orgelgehäuse hineinzunehmen und so in räumlicher Nähe zu den zu stimmenden Pfeifen aufzustellen, was das Hören erleichtert.
ZANGS Anweisung zur Herstellung der Stimmpfeife lautet so:
… Man laße sich eine viereckige hölzerne Pfeife mit einen Schieber machen, der vornen beledert ist, und den man in die Pfeife ein und ausschieben kan, wie ungefähr im allgemeinen, die Stimmpfeifen sind; sie kann 14 Zoll lang und einen Zoll weit seyn, der Schieber aber hinter der Belederung nur ¼ Zoll dick von feinen, | weißen harten Holz gemacht, und auf der obern Seite wie auch rund herum fein gehobelt. Hinten wird die Pfeife, wo der Schieber aus und eingeht, winkelrecht abgeschnitten und mit einem dünnen Bretchen das eingeleimt wird, gleich wie eine gedeckte Pfeife, versehen, dieses Brettchen wird am Ende der Pfeife, winkelrecht abgehobelt, und in der Mitte dieses Bretchens, wird das Loch viereckigt durch gemacht, durch welches der Schieber gemächlich aus und eingehet.
Nun gehet man zur Orgel und stimmt 1) in der Orgel, zum eingestrichnen C‘ das zweygestrichne C“ in einem 8füßigen Register, auf das reinste, es mag die Orgel Chorton oder Kammerton stehen.
2.) Wenn dieses geschehen, so ziehet man den Schieber der Stimmpfeife so weit heraus, und intonirt die Stimmpfeife so lange, bis man mit dem Orgel C eingestrichen, den reinsten Einklang, auf der Stimmpfeife hat. Ist solcher da, so zeichnet man mit einem Querschnittlein oben auf dem Stempel, am Loch wo der Stempfel ausgehet, sehr genau den Ton C‘ als das eingestrichne C.
3.) Nun läßt man das zweygestrichne C auf der Orgel angeben, und schiebet den Stempfel so weit in die Stimmpfeife, bis sie mit dem zweygestrichnen C“ den reinsten Einklang macht, zeichnet wie vorhin, mit einem Schnittlein oben den Stempfel auf das Genaueste am Loch, wo der Stempfel aus|geht. Wenn dieses wohl in Acht genommen wird, so wird auch die Stimmpfeife gut werden.((S. 104 ff.))
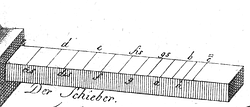
Die nächsten Punkte 4.) bis 9.) beschreiben die Herstellung eines Maßstabes, der die Strecke zwischen den beiden Marken von c‘ und c“ in 1000 Teile teilt. Der Maßstab sieht am linken Ende so aus:
Rechts setzt er sich bis 10 fort. Man findet dergleichen heute noch manchmal bei Landkarten oder auf Winkelmessern angebracht. Man kann, indem man die Zirkelspitzen in die passenden Schnittpunkte setzt, sehr gut auch die „Einer“ abgreifen und übertragen. Dazu wird eine überaus ausführliche Anleitung mit mehreren Übungsbeispielen gegeben.
Weiter mit ZANG:
10.) Die razionalgleich berechneten Theile zu den 12Tönen der eingestrichnen Oktave, bleiben den in §. 21. beschriebenen zum Monochord gehörigen gleich, nur mit dem Unterschiede, daß diese etwas größer oder kleiner werden können, und man auch hiezu einen besondern Maasstab machen mußte, daher setze ich die Zahlen nochmals hieher, nach welchen die Töne auf den Stempfel getragen werden((Die Zahlen, von SORGE übernommen, sind gerundet und fehlerfrei, wie man leicht nachrechnen kann: man dividiert die obere Zahl (Länge) durch die zwölfte Wurzel aus 2 (=1.059463); beim Fis, das die Oktave teilt, ist 1.414 = Quadratwurzel aus 2 zu finden, beim H der temperierte Halbton selbst, 1.059)).
| C Cis D Dis E F Fis | 2000 1888 von 2000 abgezogen bleibt 112 für Cis. 1782 von 2000 abgezogen bleibt 218 für D. 1682 von 2000 abgezogen bleibt 318 für Dis. 1587 von 2000 abgezogen bleibt 413 für E. 1498 von 2000 abgezogen bleibt 502 für F. 1414 von 2000 abgezogen bleibt 586 für Fis. |
Diese vom eingestrichnen C aufgetragen.|
| G Gis A B H C | 1335 davon 1000 abgezogen bleibt 335 für G. 1260 davon 1000 abgezogen bleibt 260 für Gis. 1189 davon 1000 abgezogen bleibt 189 für A. 1122 davon 1000 abgezogen bleibt 122 für B. 1059 davon 1000 abgezogen bleibt 59 für H. 1000 davon 1000 abgezogen bleibt |
Diese werden rückwärts von zweygestrichnen c aufgetragen.
11.) Nun nimmt man 112 Theile, von den verjüngten Maasstabe, und trägt sie auf den Schieber der Stimmpfeife, vornen linker Hand [die Pfeife liegt quer vor einem, der Schieber ist nach rechts herausgezogen], von dem eingestrichnen C‘ gegen die rechte Hand, nach dem zweygestrichnen c“ so gibt es das eingestrichne Cis‘.“((S. 107 f.))
Und so geht es weiter bis zu Punkt 21, wo vom c“ aus das h‘ aufgetragen wird. Wir halten fest, dass zwischen die beiden angezeichneten Marken für c‘ und c“ wie beim Monochord errechnete Marken eingezeichnet werden (wozu erst ein Maßstab erstellt werden musste, der die erforderliche 1000er-Teilung liefert.
Das Stimmen (§ 24) geht so vor sich, wie man sich das vorstellt: Nach der Stimmpfeife wird die eingestrichene Oktave eines 8-Fuß-Registers gestimmt, und nach dieser dann der Rest der Orgel.
So etwa müsste ein Grundriss aussehen.
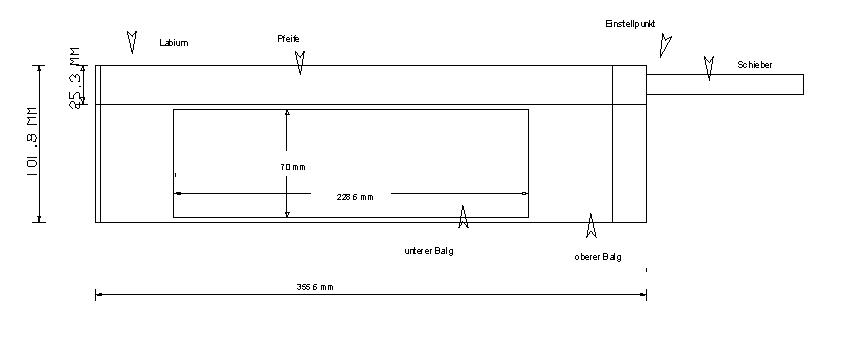
Die ganze Maschine ist 14 Zoll lang; 4 Zoll breit; 3½ Zoll hoch; 14 Zoll ist die Pfeife lang; 9 Zoll ist der untere Balg lang, und 2 3/4 Zoll breit, neben welchem die Pfeife hinter liegt. Der obere Balg, als der Gegenbalg ist 4 Zoll breit, und 11½ Zoll lang, auf welchen vornen bey M das Gewicht aufgeschraubt liegt((S. 110))
Was ist von ZANGs „Maschine“ zu halten? Durchgesetzt hat sie sich offenbar nicht, obwohl sie, folgt man ZANG, von Zangs Orgelbaumeister VOIT tatsächlich gebaut wurde und sich bewährt hat. Um sie besser zu verstehen, müssen wir ein wenig rechnen:
Bei einem Kammerton von a‘ = 440 Hz und einer Schallgeschwindigkeit von 330 m/s((Da es nur um eine Abschätzung von Größenordnungen geht, müssen wird über den absoluten ZANG-schen Kammerton und die Lufttemperaturen in den Kirchen keine Vermutungen anstellen; lag er (wahrscheinlich) statt bei 440 bei 430 oder noch tiefer, so ändert das an den im folgenden berechneten Einstellgrößen nur winzige Bruchteile.)) ist die Wellenlänge für das c‘ 126,13 cm. Eine offene Pfeife ist dann halb so lang (in Betracht kommt jetzt nur die Länge vom Aufschnitt bis zum Pfeifenende), also 63,07 cm; eine gedeckte Pfeife (um eine solche handelt es sich bei der Stimmpfeife ja) hat nur ein Viertel der Wellenlänge, also 31,53 cm. Dies ist also die Länge der Stimmpfeife ohne Fuß. Zur Oktave höher, dem c“ gehört die halbe Länge, also 15,77 cm. Der Stempel legt demnach von c‘ bis c“ die Strecke von 31,53 bis 15,77 zurück, also wieder 15,77 cm. Dies ist die Grundstrecke für den Bau des Lineals für die Teilung in 1000 Teile. 1 Teil hat also eine Länge von 0,0158 cm, das ist etwa 1/6 mm, und von diesen Teilen sind 112 für das cis‘, 218 für d‘ usw. zu nehmen und auf dem Stempel zu markieren. Setzen wir versuchsweise voraus, dies sei genau gelungen. Wie genau mit der Stimmpfeife nun wirklich gestimmt werden kann, wird davon abhängen, wie genau man den Stempel einstellen kann. Heutzutage würde man wohl einen Gewindetrieb benutzen und – wie auf der Mikrometerschraube – ganze Umdrehungen nebst Bruchteilen davon einstellen. In ZANGs Anleitung handelt es sich um Kerben, die im Schieber eingeschnitten sind und mit dem Deckel der Pfeife fluchten müssen. Nehmen wir die Mitte der Oktave, das fis‘. Dort ist ein Halbton 84 Einheiten wert, das sind 1,32 cm. Das reicht, um den Notennamen einzutragen. Gestimmt werden muss aber viel genauer. Ein Achtelton (und das ist noch ein bedeutendes Intervall) von fis‘ abwärts sind dann noch ca. 3 mm, 1 Schwebung abwärts vom temperierten fis‘ entspricht 0,6 mm. Das heißt, bei einer Genauigkeit von 1 Schwebung pro Sekunde müsste das fis‘ gerade noch einzustellen sein. Noch genauer (und auf eine halbe Schwebung sollte es schon gehen) würde es dann schon sehr schwierig.
Berechnen wir, in der selben Gegend, noch die Differenz zwischen der temperierten und der reinen Quinte g‘ zu c‘. Das c‘ hat eine Pfeifenlänge von 31,53 cm, das temperierte g‘ 21,04 cm. 2/3 von 31,53 cm sind die Länge der reinen Quinte über c‘, das sind 21,02 cm. Die Differenz der Schieberstellungen für das reine und das temperierte g‘ beträgt also 0,2 mm; das ist mit einem hölzernen Gerät kaum mehr realisierbar.
Wenn man diese feinen Einstellungen betrachtet, mag es scheinen, man gewänne durch die Stimmpfeife keine zusätzliche Sicherheit beim Stimmen. Sie hat aber einen gewichtigen Vorteil. Eine Ungenauigkeit bei einem Ton überträgt sich nicht auf die anderen, die Einstellfehler sind voneinander unabhängig. Im Gegensatz dazu vererbt sich beim Stimmen im Quintenzirkel jeder Fehler weiter.
Im praktischen Gebrauch wird man (ZANG) die Stimmpfeife wohl dazu benutzt haben, eine erste Temperierung zu stimmen; danach war es sicher zweckmäßig, die Quinten noch einmal nach Gehör abzugleichen.
ZANG hätte natürlich einfach eine längere Stimmpfeife benutzen können, etwa eine auf das kleine c statt auf c‘ eingestimmte Pfeife; damit hätte sich die Länge seiner Skala schon verdoppelt, allerdings wäre das Gerät auch nicht mehr so handlich gewesen, und das Stimmen ist bei tieferen Tönen auch schwieriger, denn die Schwebungen sind in diesem Bereich langsamer als in hohen Lagen; außerdem hätte man einen größeren Balg gebraucht.
Gegenüber der Stimmung mit dem Monochord hat die mit der Stimmpfeife den Vorteil, dass ein einigermaßen konstanter „Kammerton“ zugrunde liegt. Das c‘ der Stimmpfeife schwankt zwar mit Lufttemperatur und -Feuchte, aber es tut das in der gleichen Weise wie die Töne der Holzpfeifen in der Orgel (wenn man die Stimmpfeife in der Nähe der Orgel aufbewahrt). Ein Monochord dagegen verstimmt sich viel stärker und von den Orgelpfeifen völlig unabhängig.
Das Problem des absoluten Stimmtons blieb ungelöst. Schon wegen der von Ort zu Ort verschiedenen Längenmaße klangen sogar genau 8-füßige Pfeifen verschieden. Es gab auch noch ganz offiziell verschiedene „a’s“: Kammer- und Chorton. Die Stimmgabel war, obwohl schon 1711 von SHORE erfunden, noch nicht in Gebrauch. So musste man sich im Zusammenspiel nach dem unbeweglichsten Instrument, der Orgel, richten. Zum Orgelstimmen aber war eine Pfeife mit sauberen Markierungen sicher schon ein Fortschritt.